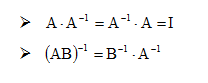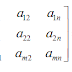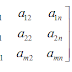Matriks adalah kumpulan bilangan atau unsur yang disusun menurut baris dan kolom. Bilangan-bilangan yang disusun tersebut disebut elemen-elemen atau komponen-komponen matriks. Nama sebuah matriks dinyatakan dengan huruf kapital. Banyak baris x banyak suatu kolom dari suatu matriks disebut ordo matriks.
Secara umum matriks dapat ditulis dengan :

Dalam hal ini aij disebut elemen matriks pada baris ke-i dan kolom ke-j.
2. Beberapa Jenis Matriks
(i) Matriks Nol (0)
Adalah matriks yang semua elemennya bernilai nol.
Adalah matriks yang semua elemennya bernilai nol.
(ii) Matriks bujur sangkar
Adalah matriks yang banyak barisnya sama dengan banyak kolomnya.
(iii) Matriks Bujur sangkarAdalah matriks yang banyak barisnya sama dengan banyak kolomnya.

(iv) Matriks Diagonal
Adalah matriks bujur sangkar yang semua elemen diluar elemen diagonal utama bernilai nol.

(v) Matriks Identitas
Adalah matriks skalar yang elemen-elemen pada diagonal utamanya bernilai satu.

(vi) Matriks Segitiga Atas
Adalah matriks bujur sangkar yang elemen-elemen dibawah diagonal utamanya bernilai nol.

(vii) Matriks Segitiga Bawah
Adalah Matriks bujur sangkar yang elemen-elemen diatas diagonal utamanya bernilai nol.

3. Operasi Matriks



4. Transpos Matriks
Transpos dari suatu matriks merupakan pengubahan baris menjadi kolom dan kolom menjadi baris. Tranpos dari matriks A dinotasikan dengan ATatau At.

Sifat : (AT) T = A
5. Determinan Matriks
Matriks yang mempunyai determinan hanyalah matriks bujur sangkar (banyaknya baris sama dengan banyaknya kolom).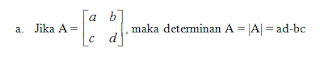

Sifat-sifat determinan matriks:

6. Invers matriks
Bila maka invers dari A adalah :
maka invers dari A adalah :

Syarat ad-bc 0
0

(v) Matriks Identitas
Adalah matriks skalar yang elemen-elemen pada diagonal utamanya bernilai satu.

(vi) Matriks Segitiga Atas
Adalah matriks bujur sangkar yang elemen-elemen dibawah diagonal utamanya bernilai nol.

(vii) Matriks Segitiga Bawah
Adalah Matriks bujur sangkar yang elemen-elemen diatas diagonal utamanya bernilai nol.

3. Operasi Matriks
- Penjumlahan atau pengurangan matriks
Matriks A dan B dapat dijumlahkan atau dikurangkan jika ordo A = ordo B

b. Perkalian Matriks dengan Skalar
Jika Skalar dikalikan dengan matriks, maka akan diperoleh sebuah matriks yang elemen- elemennya merupakan perkalian skalar tersebut dengan setiap elemen matriks.


Sifat-sifat:

c. Perkalian Dua Matriks
Dua matriks A dan B dapat dikalikan bila banyak kolom matriks pertama (kiri) sama dengan banyak baris matriks kedua (kanan).
Jika diketahui Matriks Amxn dan Bnxk maka : Jika Skalar dikalikan dengan matriks, maka akan diperoleh sebuah matriks yang elemen- elemennya merupakan perkalian skalar tersebut dengan setiap elemen matriks.


Sifat-sifat:

c. Perkalian Dua Matriks
Dua matriks A dan B dapat dikalikan bila banyak kolom matriks pertama (kiri) sama dengan banyak baris matriks kedua (kanan).


4. Transpos Matriks
Transpos dari suatu matriks merupakan pengubahan baris menjadi kolom dan kolom menjadi baris. Tranpos dari matriks A dinotasikan dengan ATatau At.

Sifat : (AT) T = A
5. Determinan Matriks
Matriks yang mempunyai determinan hanyalah matriks bujur sangkar (banyaknya baris sama dengan banyaknya kolom).
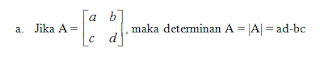

Sifat-sifat determinan matriks:

6. Invers matriks
Bila
 maka invers dari A adalah :
maka invers dari A adalah :
Syarat ad-bc
 0
0Contoh :

Jawab:

Sifat-sifat :